2017年7月No.39

リサーチ室　江森  健太郎、北脇  裕士

要約

LA–ICP–MSによる微量分析のデータを多変量解析の一種である判別分析とロジスティック回帰分析の２種類の解析法を用いて解析を行い、その解析結果の宝石鑑別への有効性について検討した。アメシストおよびルビーなどの天然・合成の鑑別には判別分析よりもロジスティック回帰分析の方がより精度が高いことが判った。しかし、交差検証の結果、合成を合成と判別できる精度は双方の解析法共に99％以上であった。パライバトルマリンの原産地鑑別においても判別分析とロジスティック回帰分析を組み合わせることにより、ブラジル産、ナイジェリア産およびモザンビーク産を高精度で判別できることが確認された。

 

■研究の背景と目的

近年の宝石鑑別にはLA–ICP–MSによる高精度の元素分析や顕微ラマン分光装置を用いた高感度のフォトルミネッセンス分析などが利用されている。このような分析技術が進展する一方で、データの解析方法も高度化が進んでいる。
分析データの取り扱いには、単変量解析、二変量解析、多変量解析と、扱う系の複雑さによる段階がある。複数の結果変数からなる多変量データを統計的に扱う多変量解析は計算負荷が高いことが障害であったが、近年のハードおよびソフトウェアの進展において活用が容易となった。しかしながら、多変量解析の宝石学における応用例はこれまで少数の報告があるのみである (文献１,２)。
本研究では、LA–ICP–MSにより得られた微量分析のデータを多変量解析の一種である判別分析とロジスティック回帰分析の２種類の解析法を用いて解析を行い、①「アメシストの天然・合成の鑑別」、②「ルビーの天然・合成の鑑別」、③「パライバトルマリンの原産地鑑別」の３つのテーマにおいてそれぞれの解析結果の有効性を検討した。

■多変量解析とは

多変量解析(multivariate analysis)とは、複数の結果変数からなる多変量データを統計的に扱う手法である。多変量解析にはおおまかに分けると、「要約」の手法と「予測」の手法がある。「要約」とは、複数の変数を新しい変数に要約する、または多くの変数を少ない変数に変換するといった手法であり、一方「予測」は複数の変数から何らかの結果を予測する、もしくは、どのような原因を作れば欲求する結果が得られるか、どのような原因でそのような結果になったのか（因果明確化）を行う手法である。宝石鑑別において、必要なものは「鑑別結果」であり、「予測」の手法を用いることになる。
予測の手法に必要なものは「目的変数」と「説明変数」である。「目的変数」とは、例えば、１つの宝石の産地といった最終的に予測したいもの、「説明変数」は、その宝石についてのデータ、例えば微量成分の濃度といったその目的変数を表現するパラメータである。既知の「目的変数」「説明変数」のデータベース(これを教師データ又はトレイニングデータと呼ぶ)から、目的変数毎に分別するための関数を作成し、その関
数を用いて、調べたい未知試料の「説明変数」から「目的変数」を求める手法が予測ということになる(図１)。

 

 

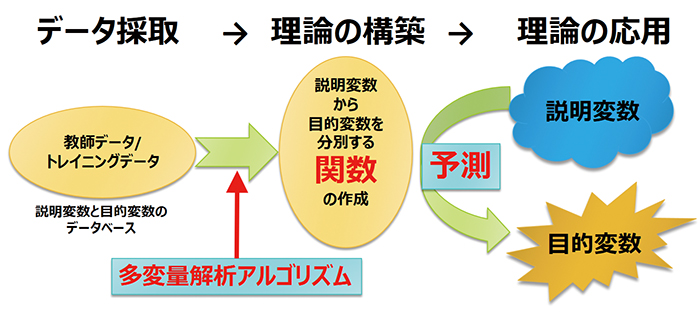
さて、予測の手法は、変数の種類によって４つの手法に分けられる。多変量解析で取り扱う変数には、「質的変数(数えることができない変数、例えば、曜日、天候等)」と「量的変数(計量可能な変数、例えば質量、長さ等)」がある。説明変数、目的変数がそれぞれ質的変数と量的変数の２種類あり、計４種類のパターンが存在することになる (表１)。 本研究では、説明変数として成分分析結果(量的変数)、目的変数として天然・合成・産地(質的変数)を扱うため、判別分析及びロジスティック回帰分析を用いる。

 

 

■判別分析とロジスティック回帰分析について
判別分析(discriminant analysis)は、事前に与えられているデータが異なるグループに分かれる場合、新しいデータが得られた際、どちらのグループに入るのかを判断するための、正規分布を前提とした分類の手法であり、1936年にロナルド・フィッシャーによって線形判別分析が発表された(文献３)。(判別分析についてはCGL通信34号「判別分析を用いた天然・合成アメシストの鑑別」をご参照下さい) 一方、ロジスティック回帰分析(logistic regression)は、ベルヌーイ分布に従う変数の統計的回帰モデルの一種で、連結関数としてロジットを使用する一般線形モデルの一種であり、1958年にデビッド・コックスにより発表された(文献４、囲み(１)参照)。判別分析と異なる点は、判別分析は事前に与えられたグループのどちらに入るのかを返り値として返すが、ロジスティック回帰分析は未知データが一方のグループに入る確率を返す点である。表２に両者の違いについてまとめた。

 

 

＝＝＝囲み(１): ロジスティック回帰分析＝＝＝

ロジスティック回帰分析は、CGL通信34号で紹介した判別分析と同じく、量的データ(質量、温度等計測可能な量)から質的データ(天然、合成といった数えることのできないパラメータ)への予測を行う多変量解析である。ベルヌーイ分布に従う変数の統計的回帰モデルの一種で、連結関数としてロジットを使用する一般線形モデルの一種でもある。
ロジスティック回帰分析は、２種類の群の判別を行い、片側の群になる確率を１、もう片側の群になる確率を０として計算を行う。
ロジスティック回帰分析では、説明変数を{x_1,i,x_2,i,x_3,i,…,x_k,i}、回帰係数を{β₀,β₁,β₂,β₃,…,β_k}、目的変数である確率をp_iとして以下の回帰式形式を用いる。

 

 

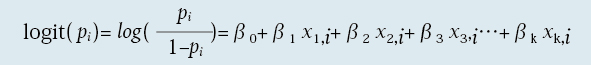
logit(p_i )が正であれば、0.5 < p < １となり、負であれば、0 < p < 0.5となる。
例えば、現在集合Xと集合Yのロジスティック回帰分析を行うと仮定する。集合Xのパラメータを回帰式に代入し、ロジット(logit(p))を得る。また、集合Yのパラメータを回帰式に代入し、ロジット(logit(q))を得る。現在、集合Xに属する確率を１、集合Yに属する確率を０とした場合、得られるlogit(p)を正、logit(q)を負となるような回帰係数を{β₀,β₁,β₂,β₃,…,β_k }を探すという計算がロジスティック回帰分析ということになる(図２)。この回帰係数を求めるために、最尤(ゆう)法というアルゴリズムを用いる。

 

 

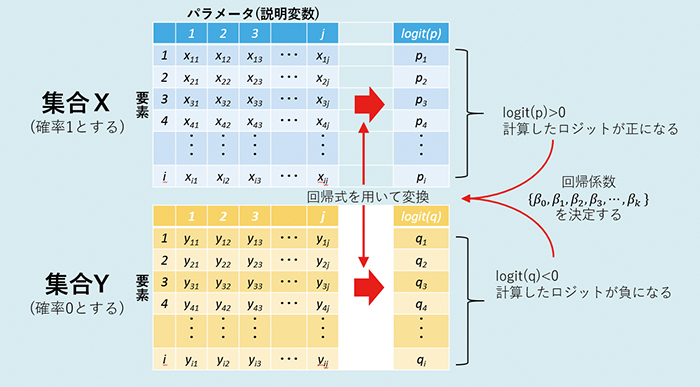
未知試料が集合X、Yのどちらに入るか知りたい場合は、ロジスティック回帰分析で得られた回帰式に未知試料の説明変数を代入し、ロジットからpを求めることで、その未知試料が集合Xに属する確率を知ることができる。
ロジスティック回帰分析は原理上集合Xと集合Yの２種類の判別にしか用いることができない。未知試料は集合Xか集合Yのどちらかに属することが前提となるため、それ以外の集合に属する可能性があるものに対しては使用できないことに注意していただきたい。
なお、本研究で提示したグラフ(図４、図７、図10)はロジスティック回帰分析で得られた回帰式に測定に用いた集合のデータを代入し、得られたそれぞれのロジット(logit(p))とロジットから計算される確率(p)をプロットしたものである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

 

■分析手法

本研究ではLA–ICP–MS装置として、LA(レーザーアブレーション装置)はNew Wave Research UP–213を、ICP–MSはAgilent 7500aを使用した。分析条件は表３に示した通りである。標準試料にはNIST612を用い、内標準として、アメシストの分析には²⁸Si、ルビー、パライバトルマリンの分析には²⁷Alを用いた。

 

 

■解析手法

分析データの解析には、R言語を用いた。R言語はオープンソース・フリーソフトウェアの統計解析向けのプログラミング言語及びその開発実行環境である。使用可能なパッケージが多く、統計学を超えて学問分野や業界を問わず、金融工学・時系列分析・機械学習・データマイニング・バイオインフォマティクス等、柔軟なデータ解析や視覚化そして知識共有の需要に応え得るR言語の普及は世界的な広がりを見せている。本研究において、判別分析は、Rに提供されるMASSパッケージのlda関数、ロジスティック回帰分析にはglm関数を用いた。

 

■結果及び考察

１. アメシストの天然・合成の鑑別
<サンプルと分析方法>
天然アメシスト50点、合成アメシスト49点を分析に用いた。天然アメシスト50点の中で、産地が既知のサンプルは、ブラジル産10点、ザンビア産６点、日本産２点、ニュージーランド産１点、また合成アメシストは日本製５点、ロシア製4点を含み、ブラジルや国内市場で流通している市場性が高いサンプルを用いた。サンプルはすべてファセットカットされており、ブラジル産天然アメシスト５点、ザンビア産天然アメシスト６点については、LA–ICP–MSで５点ずつ分析を行い、その他のサンプルについては２点ずつ分析を行った(図３)。

 

 

 

＜分析結果と考察＞
天然アメシスト、合成アメシストの分析データを用いて判別分析を行った。判別分析には測定に用いた元素(⁷Li, ⁹Be, ¹¹B, ²³Na, ²⁷Al, ³⁹K, ⁴⁵Sc, ⁴⁷Ti, ⁶⁶Zn, ⁶⁹Ga, ⁷²Ge, ⁹⁰Zr, ²⁰⁸Pb)を使用した。扱う群は天然・合成の2群であり、判別得点は１つでもよいのであるが、２次元に拡張を行い、計算を行った。得られた判別関数は、

 

LD1 =  –0.0684[Li]+0.001255[Be]+0.220764[B]–0.03541 [Na]+0.005085[Al]+0.007468[K]+0.022369 [Sc]
–0.00737[Ti]–0.03682[Zn]–0.09037[Ga]–0.09037[Ge]–0.03376[Zr]–0.00072[Pb]
LD2 =  –0.09304[Li]–0.164546[Be]–0.17436[B] +0.005201[Na]–0.019521[Al]–0.00033[K]–0.13679[Sc]
+0.011894[Ti]+0.009492[Zn]+046953[Ga] –1.17219[Ge]–0.07558[Zr]+0.002117[Pb]

 

となった。なお、括弧[元素記号]で囲われた部分は、その元素記号で表した元素の濃度(ppmw)を示す。上記関数に天然・合成アメシストの分析値を代入し、プロッティングを行ったグラフを図４に示す。

 

 

また、同じデータを用いて、ロジスティック回帰分析を行った。天然を１、合成を０とし、ロジットを求める回帰式を計算した結果、

 

logit(p) =　–0.38475[Li]+55.56693[Be]–13.2438[B]+2.1611[Na]–0.18751[Al]–0.93194[K]+0.89311[Sc]
–1.51653[Ti]+0.42607[Zn]+16.56753[Ga]+5.61131[Ge]+60.20579[Zr]–0.05453[Pb]+2.81222

 

が得られた。判別分析同様、括弧[元素記号]で囲われた部分は、その元素記号で表した元素の濃度(ppmw)を示す。上記関数に分析値を代入し得られたlogit(p)と天然アメシストである確率ｐについてグラフを作成した結果を図４に示す。ロジスティック回帰分析の結果は、本来は図５のようなプロットを行わないが、ビジュアル的にわかりやすくするため、logit(p)とpでグラフを表記した。

 

 

判別分析、ロジスティック回帰分析共に天然・合成の乖離（かいり）が良く、非常によい解析結果に見える。そこでデータの解析の精度について確認を行うため、交差検証(Cross-validation)を行った。交差検証は統計学において標本データを分割し、その一部をまず解析し、残る部分で解析のテストを行うことで、解析自身の妥当性の検証、確認に当てる手法を差す(交差検証については囲み(２)参照)。今回の解析について、交差検証を行った結果を表４に示す。

 

 

誤判別率(間違って判別する確率)を計算すると、判別分析は10.3%、ロジスティック回帰分析は1.7%という結果が得られ、ロジスティック回帰分析の誤判別率が低く、優位な結果が得られた。しかし、判別分析、ロジスティック回帰分析共に合成アメシストを合成アメシストであると判断する確率は99.0%と、合成石をチェックするにはよい手法ではないかと思われる。

 

＝＝＝囲み(２): 交差検証(Cross–validation)とは＝＝＝

交差検証(Cross–validation)とは、データの解析(導出された推定や統計的な予測)がどれだけ母集団に対処できるかを検証・確認する方法で、標本データを分割し、一部をまず解析し、残る部分で解析のテストを行い、解析自身の妥当性の検証・確認を行う手法である。一般的に交差検証は、それ以上標本を集めることが困難である場合に、推定の裏付けを行う際に必要な手法だとされている。
交差検証の手法には主に「ホールドアウト検証」、「k–分割交差検証」、「leave–one–out交差検証」が知られており、本研究では「leave–one–out交差検証」を用いたが、「leave–one–out交差検証」は「k–分割交差検証」の特別な場合であるため、まず「k–分割交差検証」について説明を行う。
「k–分割交差検証」では、まず、標本群をk個に分割する。そのうちの１個をテスト事例(testing group)、残りの(k–1)個を訓練事例(training group)とする。(k–1)個の訓練事例(training group)を用いて、判別分析及びロジスティック回帰分析を行い、テスト事例(testing group)のテストを行う(図６)。これをk回行った結果から検証をし、１つの推定を得る手法である。

 

 

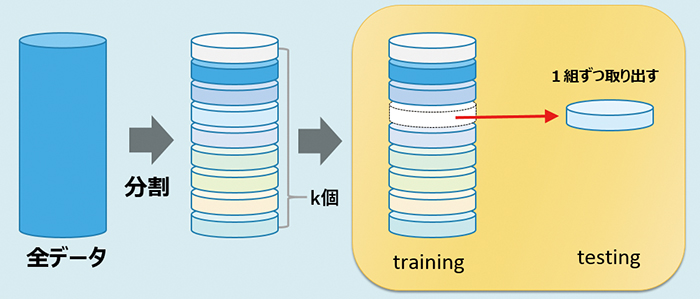
「leave–one–out交差検証」は、kが標本数とイコールの場合の交差検証である。すなわち、標本群から１標本をテスト事例(testing group)とし、残りの標本すべてを訓練事例(testing group)として判別分析もしくはロジスティック回帰分析を行い、テスト事例とした１標本の調査、検証を行う。この検証を標本数だけ行い、推定結果の調査を行う手法である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

 

２. ルビーの天然・合成の鑑別
＜サンプルと分析方法＞
天然ルビー174点、合成ルビー28点を分析に用いた。天然ルビーは産地別にミャンマー52点、タイ28点、モザンビーク28点、タンザニア26点、ベトナム17点、カンボジア15点、マダガスカル４点、スリランカ４点、また合成ルビーは製造方法別にフラックス法12点、FZ法６点、ベルヌイ法５点、熱水法３点、結晶引上法２点である。天然ルビーに関してはサンプル毎に３〜５点、合成ルビーに関しては各５点ずつ分析を行った(図７)。

 

 

 

＜分析結果と考察＞
天然ルビー、合成ルビーの分析データを用いて判別分析を行った。判別分析には測定に用いた元素(²⁴Mg, ⁴¹Ti, ⁴⁷V, ⁵³Cr, ⁵⁷Fe, ⁶⁹Ga)を使用した。扱う群は天然・合成の２群であり、判別得点は１つでもよいのであるが、２次元に拡張を行い、計算を行った。得られた判別関数は、

 

LD1 =  –0.01013[Mg]+0.000758[Ti]–0.01378[V]–0.00021[Fe]–0.000074785[Ga]
LD2 =  0.003816[Mg]–0.00293[Ti]+0.003421[V]–0.0006[Fe]–0.00433621[Ga]

 

となった。なお、括弧[元素記号]で囲われた部分は、その元素記号で表した元素の濃度(ppmw)を示す。上記関数に天然・合成ルビーの分析値を代入し、プロッティングを行ったグラフを図８に示す。

 

 

また、同じデータを用いて、ロジスティック回帰分析を行った。天然を１、合成を０とし、ロジットを求める回帰式を計算した結果、

 

logit (p) =  1.5042[Mg]–6.2345[Ti] +90.9248[V]+0.1373[Fe]+0.3736[Ga]–131.038

 

が得られた。判別分析同様、括弧[元素記号]で囲われた部分は、その元素記号で表した元素の濃度(ppmw)を示す。上記関数に分析値を代入して得られたlogit(p)と天然ルビーである確率pについてグラフを作成した結果を図９に示す。

 

 

判別分析、ロジスティック回帰分析共に天然・合成の乖離（かいり）が良く、非常によい解析結果に見える。そこでデータの解析の精度について確認を行うため、交差検証(Cross–validation)を行った。今回の解析について、交差検証を行った結果を表５に示す。

 

 

誤判別率(間違って判別する確率)を計算すると、判別分析は10.5%、ロジスティック回帰分析は1.5%とよい結果が得られ、ロジスティック回帰分析の誤判別率が低く、優位な結果が得られた。検証の結果、判別分析、ロジスティック回帰分析共に合成ルビーを合成であると正しく判断する確率は99.0%であり、合成石の検出には優れた手法であることが確認できた。

 

3. パライバトルマリンの原産地鑑別
＜サンプルと分析方法＞
ブラジル産パライバトルマリン186点、モザンビーク産パライバトルマリン44点、ナイジェリア産パライバトルマリン11点をサンプルとして用いた。ブラジル産はバターリャ鉱山産79点、ムルング鉱山産60点、キントス鉱山産47点を用い、ナイジェリア産は業者間でタイプ１と呼ばれる色や外観がブラジル産と酷似しているものを分析に用いた(図10)。以降、便宜上ナイジェリア産タイプ１をナイジェリア産と呼ぶことにする。色はBlue、Green Blue、Blue Green系のサンプルを使用し、Greenの強いものは除外した。

 

 

 

 

＜分析結果と考察＞
ブラジル産、モザンビーク産、ナイジェリア産タイプ１パライバトルマリンについて判別分析を行った。ブラジル産については、バターリャ、キントス、ムルングと３つの鉱区のトルマリンについてのデータがあるが、ブラジル産と一括して分析を行った。判別分析には⁹Be, ⁶⁹Ga, ⁷²Ge, ⁹³Nb, ¹²¹Sb, ¹⁸¹Ta, ²⁰⁸Pbの７種類の元素を用いた。得られた判別関数は、

 

LD1 =  –0.0265[Be]+0.0016[Ga]+0.0345[Ge]–0.5621[Nb]–0.0075[Sb]+0.0574[Ta]–0.0035[Pb]
LD2 =  –0.0025[Be]–0.0003[Ga]+0.0108[Ge]–0.4911[Nb]–0.0469[Sb]–0.0709[Ta]+0.0079[Pb]

 

となった。なお、括弧[元素記号]で囲われた部分は、その元素記号で表した元素の濃度(ppmw)を示す。上記関数に各産地のパライバトルマリンの分析値を代入し、得られた結果を図11に示す。

 

 

オーバーラップする部分はあるものの、ブラジル、モザンビーク、ナイジェリアの３つの産地の乖離がよいように見える。この解析結果について、交差検証を行った結果を表６に示す。

 

 

交差検証を行った結果、モザンビーク産の70.5%、ナイジェリア産タイプ１の全てがブラジル産であると判定されるという結果になった。グラフ上は乖離（かいり）しているが、判別分析アルゴリズム上はこの３産地の区別は非常に難しいという結果となった。
さらに、同データを使用したロジスティック回帰分析を用いて、２産地の判別を行った。ブラジル産とモザンビーク産、ブラジル産とナイジェリア産タイプ１、モザンビーク産とナイジェリア産タイプ１のロジスティック回帰分析、そしてその交差検証を行った結果を図12と表７に示す。

 

 

表７ パライバトルマリンの２産地比較におけるロジスティック回帰分析の交差検証結果

 

 

 

 

ロジスティック回帰分析による２産地比較は乖離（かいり）が非常によく、交差検証結果も良好である。ナイジェリア産タイプ１については分析に用いた試料が11点と少ないため、今後サンプル数を増やし、精度の向上を図る必要があるが、一般的な鑑別手法等を用いて２産地にまで絞り込むことができれば、この手法は非常に有効な手法になり得るであろう。

 

■まとめ

量的データから質的データの予測を行う多変量解析である「判別分析」「ロジスティック回帰分析」を用いた「アメシストの天然・合成の鑑別」「ルビーの天然・合成の鑑別」「パライバトルマリンの原産地鑑別」の可能性について調査を行った。アメシスト及びルビーの天然・合成の鑑別については、微量成分分析結果を用いたロジスティック回帰分析による判別が有効であることが判った。今回の調査により判別分析を用いても合成を合成、天然を天然と正しく判断する確率はきわめて良好であり、合成石の確認には優れているということが確認できた。「パライバトルマリンの原産地鑑別」については、判別分析による結果はグラフで見ると乖離（かいり）はよいが、交差検証による評価は低かった。一方、２産地比較におけるロジスティック回帰分析による乖離（かいり）は良好であった。従って、これらの双方の解析法を適宜組み合わせて使用する事が望ましいと思われる。
多変量解析による宝石鑑別は有効な手法ではあるが、ブラックボックスを扱うため、単体での使用は危険であり、一般的な鑑別手法と組み合わせて使うことが好ましい。◆

 

■参考文献
文　献１：Blodgett T., Shen. A., 2011, Application of discriminant Analysis in gemology: country-of-origin separation in 　　　　　colored stones and distinguishing HPHT-treated diamonds, Gems & Gemology, Summer 145
文　献２：Luo Z., Yang M., Shen A., 2015, Origin determination of dolomite-related white nephrite through
iterative-binary linear discriminant analysis, Gems & Gemology, Fall 300-311
文　献３：Fisher, R.A., 1936, The use of multiple measurements in taxonomic problems. Annals of Eugenics, 7, 179-188
文　献４：Cox, D.R., 1958, The Regression Analysis of Binary Sequences. Journal of the Royal Statistical Society Series B
(Methodological), 20(2), 215-242

また、今回解析に利用した統計解析ソフトRはhttps://cran.r-project.org/からダウンロード可能。対応OSはWindows、Mac OS、Linux (2017.7.25.現在)